5. Parallel Axis Theorem

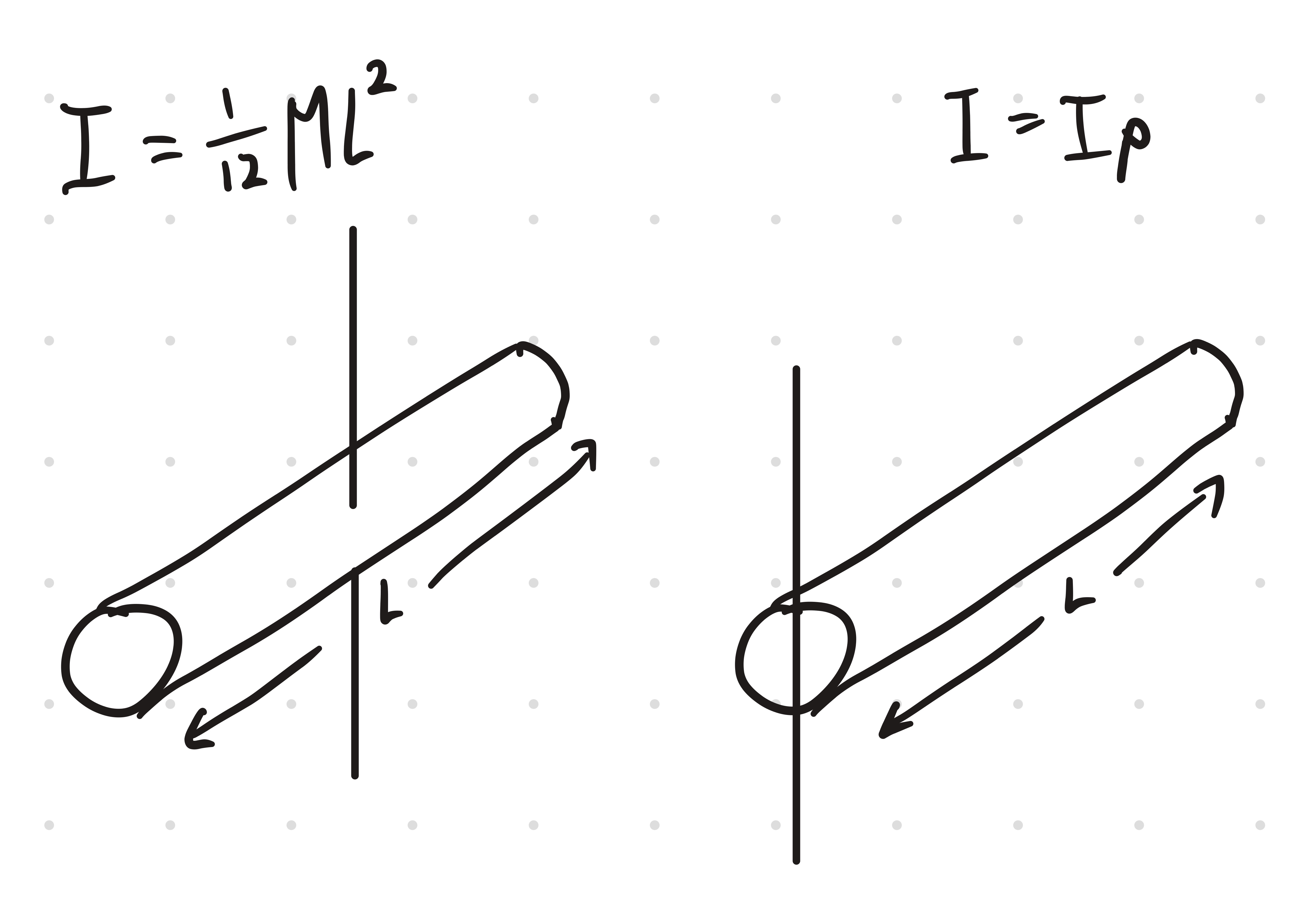
Definitions

Parallel Axis Theorem

• A theorem that relates the moment of inertia about any axis to the moment of inertia about a parallel axis through the center of mass

$$I_p = I_{cm} + Md^2$$

where $I_p$ is the moment of inertia around the rotation axis, $I_{cm}$ is the moment of inertia around the centre of mass, $M$ is the total mass, and $d$ is the distance between the two parallel axes

 

Derivations

objects don't always rotate around the most convenient axis

the parallel axis theorem states that

$$I_p = I_{cm} + Md^2$$

where $I_p$ is the moment of inertia about a parallel axis at distance $d$ from the center of mass

this allows us to calculate the moment of inertia about any parallel axis if we know the moment of inertia about the center of mass

 

Useful Equations

$$I_p = I_{cm} + Md^2$$

 

Example 1

A slender rod of mass $M$ and length $L$ rotates about an axis through one end. Given that $I_{cm} = \frac{1}{12}ML^2$, what is the moment of inertia about the end?

Answer

Using the parallel axis theorem with $d = \frac{L}{2}$

$$I_p = I_{cm} + Md^2$$ $$I_p = \dfrac{1}{12}ML^2 + M\left(\dfrac{L}{2}\right)^2$$ $$I_p = \dfrac{1}{12}ML^2 + \dfrac{1}{4}ML^2$$ $$I_p = \dfrac{1}{3}ML^2$$

 

Example 2

A disc of mass 5 kg has a moment of inertia about its center of 0.5 kg⋅m². What is its moment of inertia about an axis parallel to the center axis but 0.2 m away?

Answer

Using $I_p = I_{cm} + Md^2$

$$I_p = 0.5 + 5(0.2)^2$$ $$I_p = 0.5 + 5(0.04) = 0.5 + 0.2 = 0.7 \text{ kg⋅m}^2$$