3. Angular Acceleration

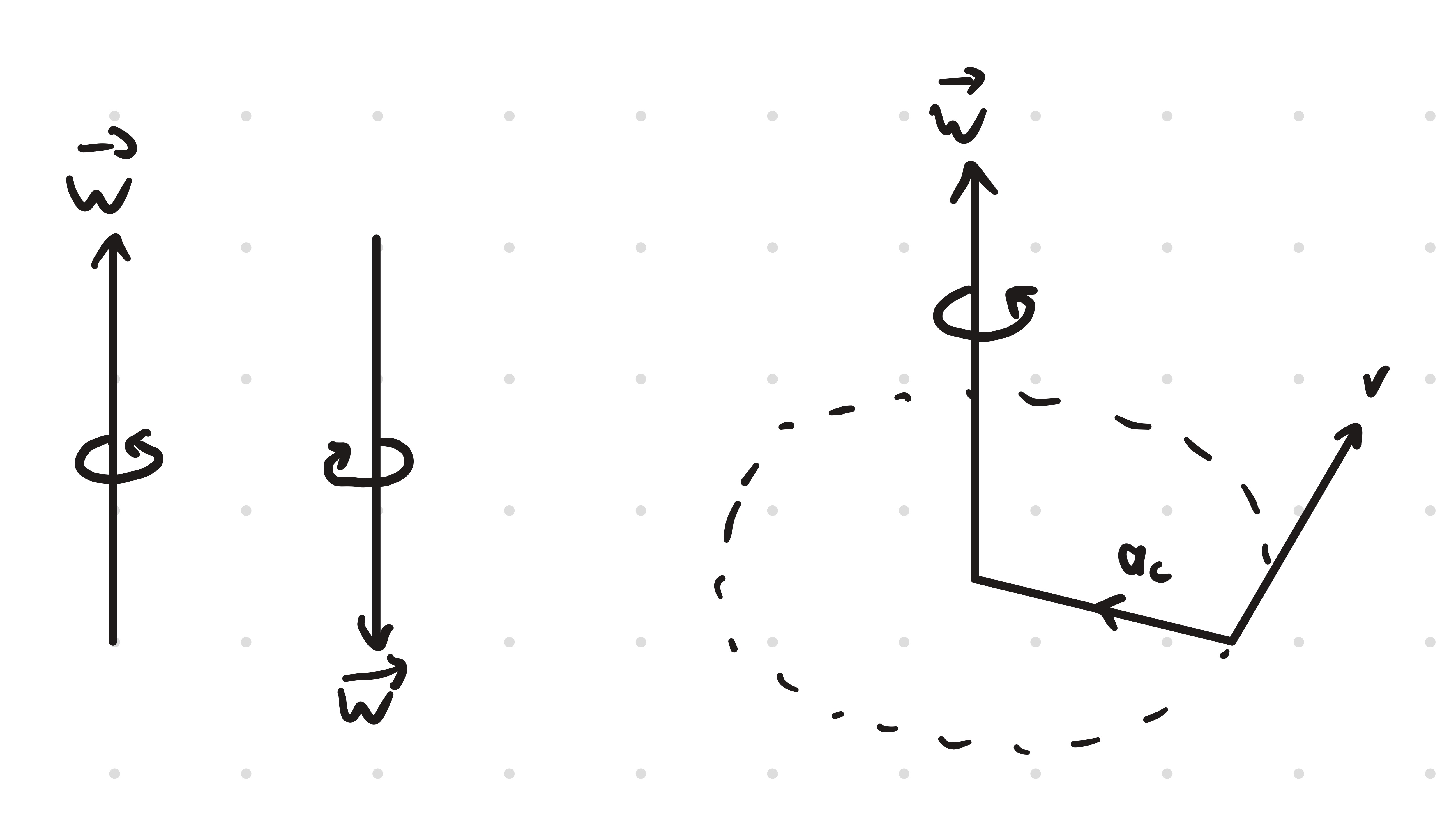
Definitions

Angular Acceleration (α)

• Rate of change of angular velocity, measured in rad/s²

$$\alpha = \dfrac{\Delta \omega}{\Delta t}$$

Tangential Acceleration

• Changes the magnitude of the angular velocity

Radial (Centripetal) Acceleration

• Points toward the centre of the circular path and changes the direction of the velocity

 

Derivations

by definition, angular acceleration is

$$\alpha = \dfrac{\Delta \omega}{\Delta t}$$

taking the limit as $\Delta t \to 0$

$$\alpha = \lim_{\Delta t \to 0} \dfrac{\Delta \omega}{\Delta t} = \dfrac{d\omega}{dt}$$

for an object moving in a circle, acceleration can be decomposed into two components

$$\vec{a} = \begin{pmatrix} a_t \\ a_c \end{pmatrix}$$

deriving $a_t$ and $a_c$, starting with

$$v = \omega r$$

take the derivative with respect to time

$$\dfrac{dv}{dt} = \dfrac{d\omega}{dt}r + \omega\dfrac{dr}{dt}$$

this can be rewritten as

$$a = \alpha r + \omega\dfrac{dr}{dt}$$

therefore, the radial (centripetal) acceleration is

$$a_c = \alpha r$$

and the tangential acceleration is

$$a_t = \omega\dfrac{dr}{dt}$$

 

Constant Angular Acceleration

assuming constant angular acceleration

$$\alpha = \text{constant}$$ $$d\omega = \alpha dt$$

integrate both sides

$$\int_{\omega_0}^{\omega} d\omega = \int_{0}^{t} \alpha \, dt$$ $$\omega - \omega_0 = \alpha t$$ $$\boxed{\omega = \omega_0 + \alpha t}$$

if we solve for $\theta$

$$\dfrac{d\theta}{dt} = \omega_0 + \alpha t$$ $$\int_{\theta_0}^{\theta} d\theta = \int_{0}^{t} (\omega_0 + \alpha t)\, dt$$ $$\theta - \theta_0 = \omega_0 t + \frac{1}{2}\alpha t^2$$ $$\boxed{\theta = \theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2}$$

 

Useful Equations

$$\alpha = \dfrac{d\omega}{dt}, \quad a_c = \alpha r, \quad a_t = \omega\dfrac{dr}{dt}$$ $$\omega = \omega_0 + \alpha t$$ $$\theta = \theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2$$

 

Example 1

A wheel starts from rest and accelerates with a constant angular acceleration of 2 rad/s². What is its angular velocity after 5 seconds?

Answer

Using $\omega = \omega_0 + \alpha t$ with $\omega_0 = 0$

$$\omega = 0 + 2 \times 5 = 10 \text{ rad/s}$$

 

Example 2

A disc rotates with an initial angular velocity of 4 rad/s and angular acceleration of 3 rad/s². How many radians does it rotate through in 2 seconds?

Answer

Using $\theta = \theta_0 + \omega_0 t + \frac{1}{2}\alpha t^2$ with $\theta_0 = 0$

$$\theta = 0 + 4(2) + \frac{1}{2}(3)(2)^2$$ $$\theta = 8 + 6 = 14 \text{ rad}$$