2. Circular Motion

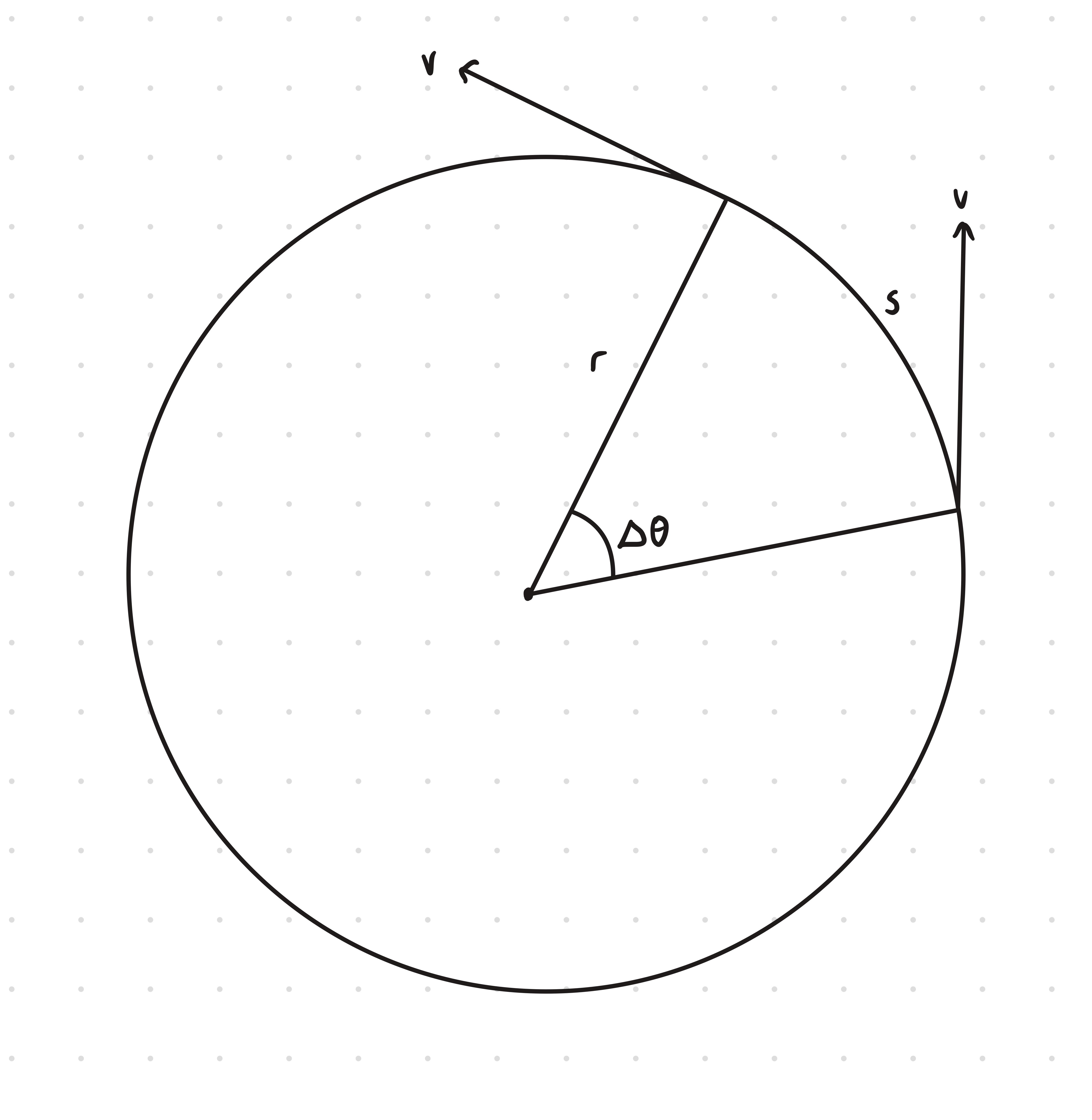
Definitions

Angular Velocity (ω)

• Rate of change of angular displacement, measured in rad/s

Centripetal Acceleration

• Acceleration directed toward the center of circular motion, $a = \frac{v^2}{r}$

Centripetal Force

• Net force directed toward the center that keeps an object in circular motion, $F = \frac{mv^2}{r}$

 

Derivations

starting with arc length and linear displacement

$$s = \Delta \theta r$$ $$s = v \Delta t$$

equating these expressions

$$v \Delta t = \Delta \theta r$$

rearranging

$$\dfrac{v}{r} = \dfrac{\Delta \theta}{\Delta t}$$

by definition, angular velocity is the rate of change of angular displacement

$$\omega = \dfrac{\Delta \theta}{\Delta t}$$

taking the limit as $\Delta t \to 0$

$$\omega = \lim_{\Delta t \to 0} \dfrac{\Delta \theta}{\Delta t} = \dfrac{d\theta}{dt}$$

therefore, the relationship between linear and angular velocity is

$$v = \omega r$$

 

Useful Equations

$$\omega = \frac{\theta}{t}, \quad s = \theta r, \quad v = \omega r$$ $$a = \frac{v^2}{r} = \omega^2 r$$ $$F = \frac{mv^2}{r} = m\omega^2 r$$

 

Example 1

A particle moves in a circle of radius 2 m with angular velocity 3 rad/s. What is its linear velocity?

Answer

Using $v = \omega r$

$$v = 3 \times 2 = 6 \text{ m/s}$$

 

Example 2

A car travels around a circular track of radius 50 m at 20 m/s. What centripetal acceleration does it experience?

Answer

Using $a = \frac{v^2}{r}$

$$a = \frac{20^2}{50} = \frac{400}{50} = 8 \text{ m/s}^2$$