5. Distributed Mass Pendulum

Definitions

Distributed Mass Pendulum

• A pendulum whose mass is spread along its length rather than concentrated at a point.

 

Derivations

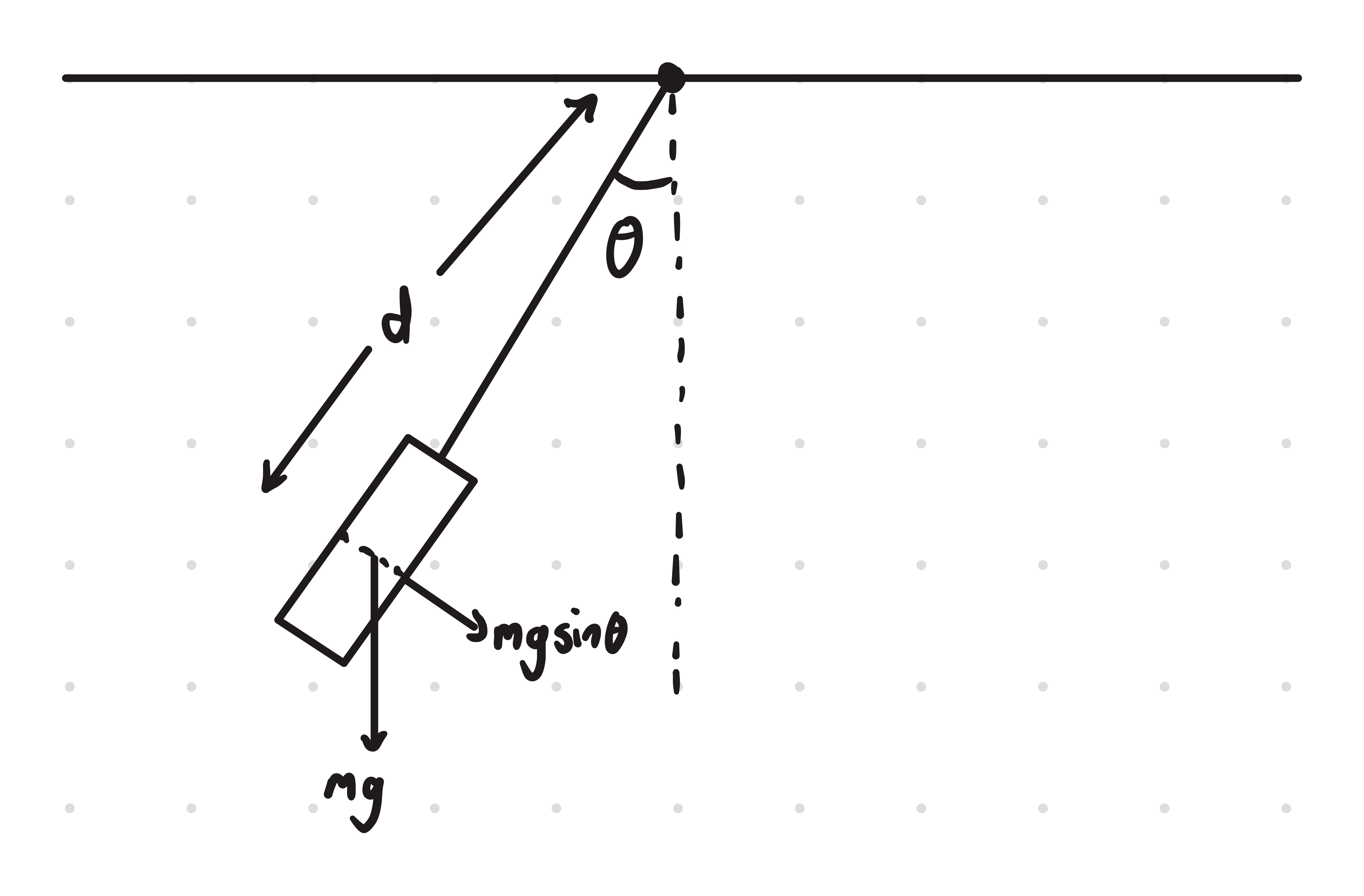
Angular Velocity

Restoring force

$$\tau = -mgdsin(\theta)$$

for small angles

$$sin(\theta) = \theta$$

therefore

$$\tau = -mgd\theta, \quad \tau = I\ddot{\theta}$$

so

$$I\ddot{\theta} + mgd\theta = 0$$

rewritten we get

$$\ddot{\theta} = -\dfrac{mgd}{I}\theta$$

this is in the form of a SHM therefore

$$\omega^2 = \dfrac{mgd}{I}$$

Kinetic Energy

Since

$$v = \omega r, \quad dK = \dfrac{1}{2}v^2 \; dm$$

we can write the kinetic energy as

$$dK = \dfrac{1}{2}r^2\omega^2 \; dm$$

integrate both sides

$$K = \dfrac{1}{2}\omega \int{r^2 \; dm} = \dfrac{1}{2}I\omega^2$$

 

Useful Equations

 

Example 1

A physical pendulum consists of a thin, uniform rod of length $L$. The rod is pivoted at one end and undergoes small oscillations.

Calculate the period of oscillation.

Answer

Moment of inertia of a rod

$$I = \dfrac{1}{3}mL^2$$

equation for period

$$T = 2\pi \sqrt{\dfrac{I}{mgd}}$$

$d$ is the distance to the centre of mass so

$$d = \dfrac{1}{2}L$$

subbing $I$ and $d$ into the equation for the period

$$T = 2\pi \sqrt{\dfrac{\dfrac{1}{3}mL^2}{mg \dfrac{1}{2}L}}$$

simplify

$$T = 2\pi \sqrt{\dfrac{2}{3} \dfrac{L}{g}}$$

 

Example 2

A physical pendulum consists of a thin, uniform rod of length $L$ and mass $m$, pivoted at one end. At a given instant, the rod has angular speed ($\omega$)

Calculate the kinetic energy of the rod.

Answer

Moment of inertia for a uniform rod

$$I = \dfrac{1}{3}mL^2$$

sub $I$ into kinetic energy equation

$$K = \dfrac{1}{2}(\dfrac{1}{3}mL^2)\omega^2$$

therefore

$$K = \dfrac{1}{6}mL^2\omega^2$$