4. Pendulums

Definitions

Torsional Pendulum

• A system twisted by a small angular displacement $\theta$ due to torque

Simple Pendulum

• A system consisting of a point mass suspended by a rod or string of negligible mass

Derivations

Torsional Pendulum

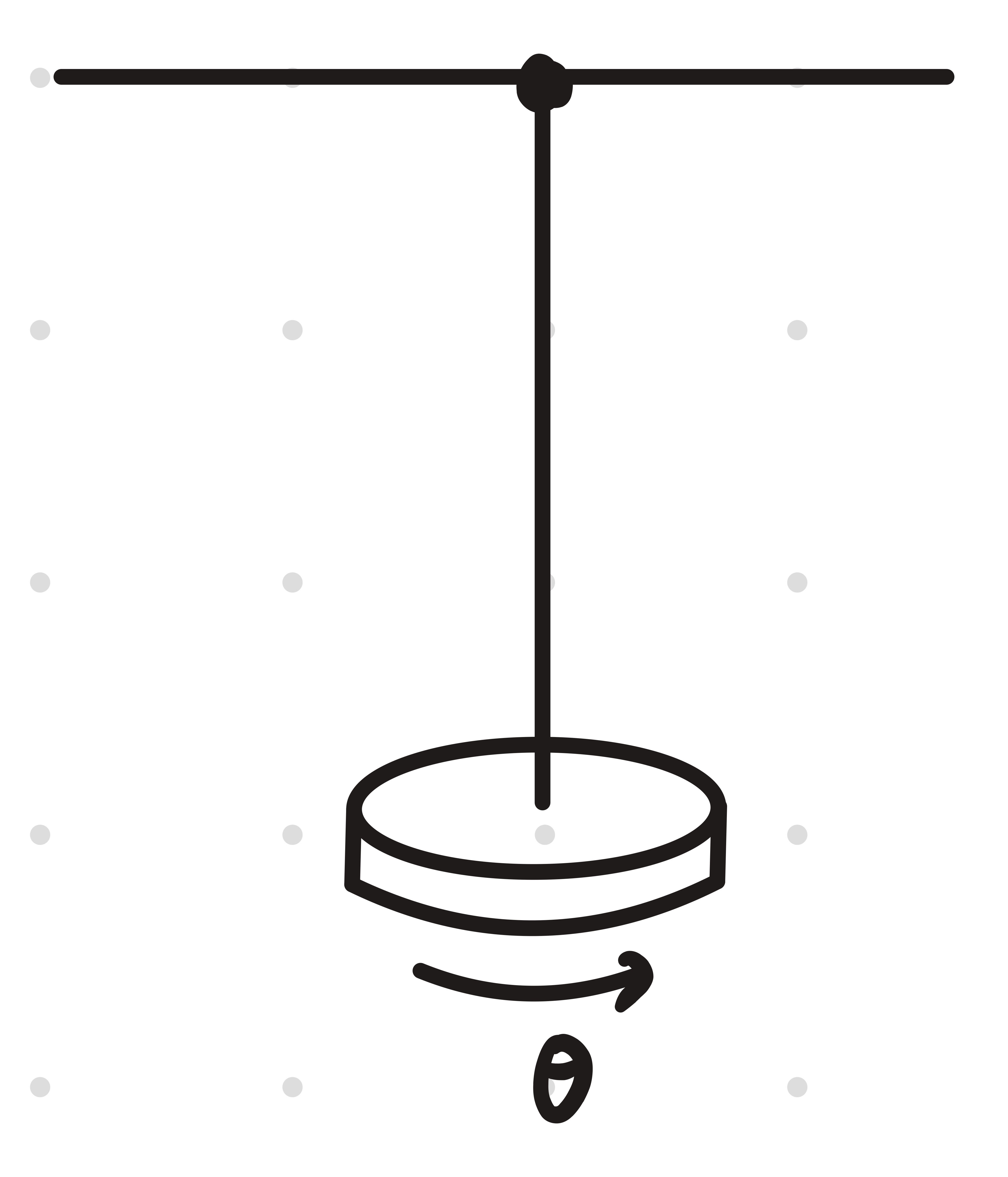
We define

$$\tau_z = -k\theta$$

where $k$ is the torsion constant

since

$$\tau_z = I\alpha_z = I\ddot{\theta}$$

equating $\tau_z$

$$\ddot{\theta} = -\dfrac{k}{I} \theta$$

this is in the form of SMH therefore

$$\omega^2 = \dfrac{k}{I}, \quad \omega = \sqrt{\dfrac{k}{I}}$$

 

Simple Pendulum

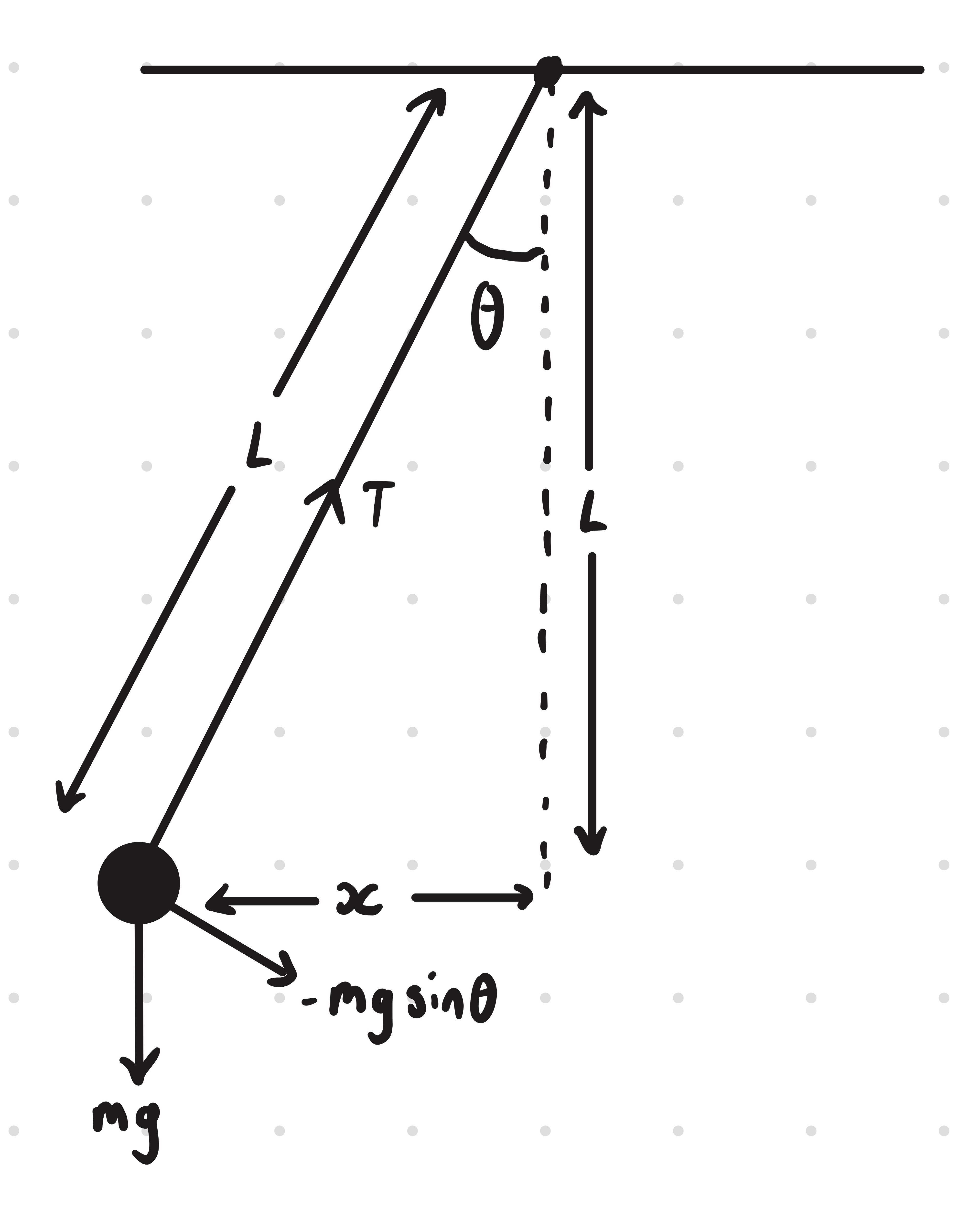
We can see that

$$sin(\theta) = \dfrac{x}{L}$$

where $\theta$ is in radians

assuming $\theta$ is small

$$\theta \approx \dfrac{x}{L}$$

therefore the restoring force is

$$F \approx -mg \dfrac{x}{L}$$

since $\dfrac{mg}{L}$ is constant we define $k$ as this constant such that

$$F \approx -kx$$

solving for $\omega$, we can divide both sides by $m$

$$a = -\dfrac{k}{m}x$$

therefore

$$\omega = \sqrt{\dfrac{k}{m}}$$

subbing $k = \dfrac{mg}{L}$

$$\omega = \sqrt{\dfrac{g}{L}}$$

Why don't we account for tension $T$

• String doesn't change length
• Bob moves in a circular arc
• So tension is always perpendicular to displacement

$$T \cdot s = 0$$

where $s$ is the displacement along the path (arc length)

therefore no work done by tension