4. Gravitational Potential

Definitions

Gravitational Potential

• The energy an object posses due to its position in a gravitational field
• Gravitational potential energy per mass at a that point
• Work done per unit mass in bringing a mass from infinity to a defined point
• Always negative

Derivations

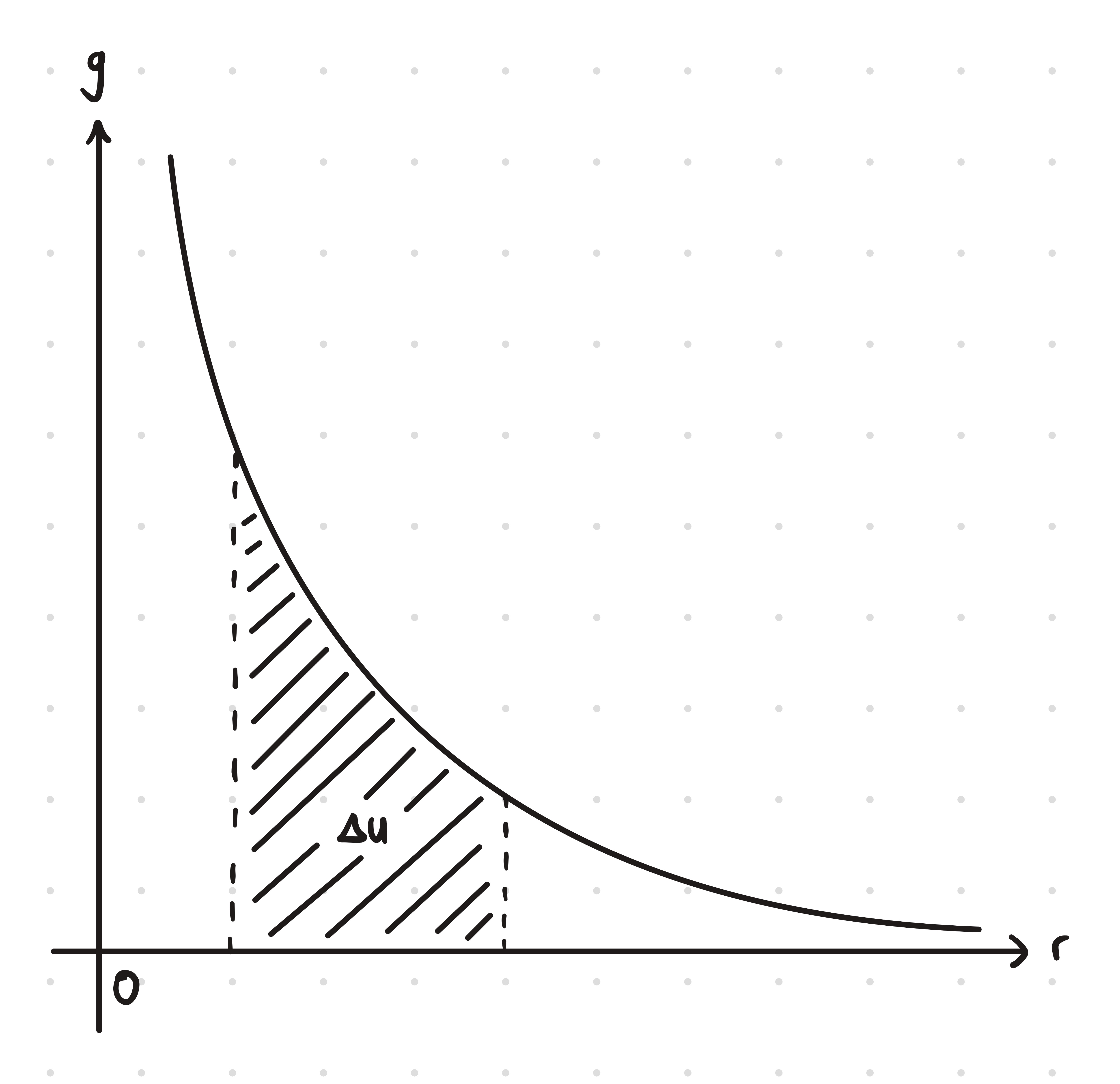
The area under the graph g-r gives you the change in gravitational potential

Work Done

Since gravitational potential equals work done per unit mass $W = Fr$

$$U(r) = - \dfrac{Fr}{m}$$

subbing in $F = \dfrac{GMm}{r^2}$

$$U(r) = - \dfrac{GM}{r} \quad \quad (\text{Jkg}^{-1})$$

Integration Method

Since the change in gravitational potential is the area under the graph g-r

$$g = -\dfrac{GM}{r^2}$$

integrating

$$U(r) = \int_{r}^{\infty} -\dfrac{GM}{r^2} \; dr$$

this results in

$$U(r) = [\dfrac{GM}{r}]_{r}^{\infty}$$

which looks like

$$U(r) = \dfrac{GM}{\infty} - \dfrac{GM}{r}$$

which simplifies to

$$U(r) = -\dfrac{GM}{r} \quad \quad (\text{Jkg}^{-1})$$

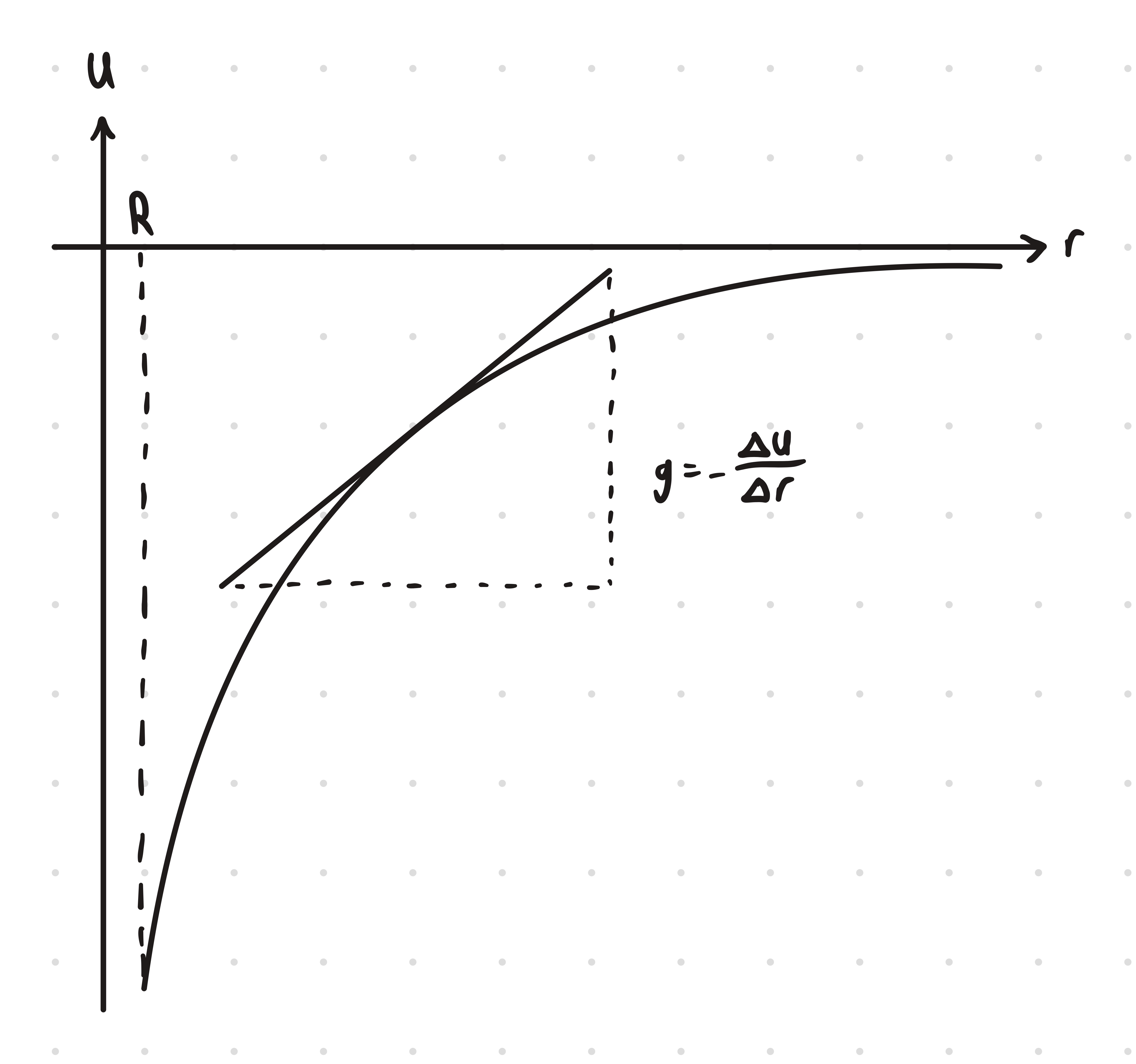
Gradient of U-r

Furthermore if you calculate the gradient of U-r you get $g$

Useful Equations

$$U(r) = -\dfrac{GM}{r}$$