2. Time Dialation

Definitions

Inertial Frame

• An inertial frame of reference is one which bodies move in a straight line at constant speeds

• Different frames of reference move relative to one another

Einstein's Postulates

• Physics laws have the same form in all inertial frames

• The speed of light in free space is invariant

Proper Time

• $t_0$ time for stationary observer

Observer at constant ($v$)

• $t$ time measured in frame of observer

Lorentz Factor

• $\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$ where $v$ is relative velocity and $c$ is the speed of light

• Relates measurements between different inertial reference frames

• Appears in time dilation equation: $t = \gamma t_0$

• $\gamma > 1$

 

Derivations

Imagine if someone on a train shone a light on a mirror such that the light travelled in a straight line

Frame 1: Proper Time

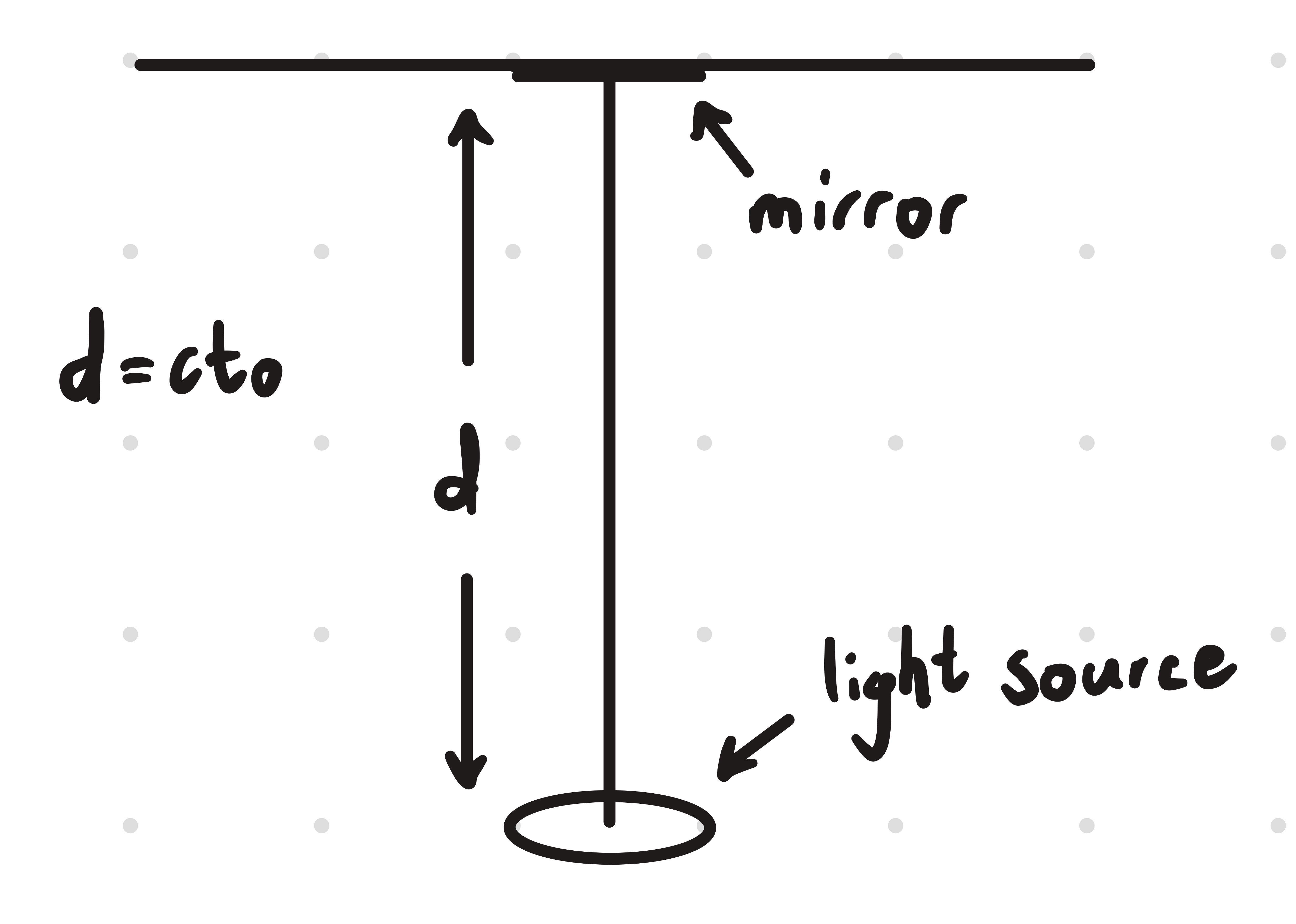
If someone outside the train where to view the path of light, it would travel at an angle.

This means the light would travel further

However since the speed of light is constant, the time taken for the light to travel its respective distance, must be longer

Frame 2: Observer Time

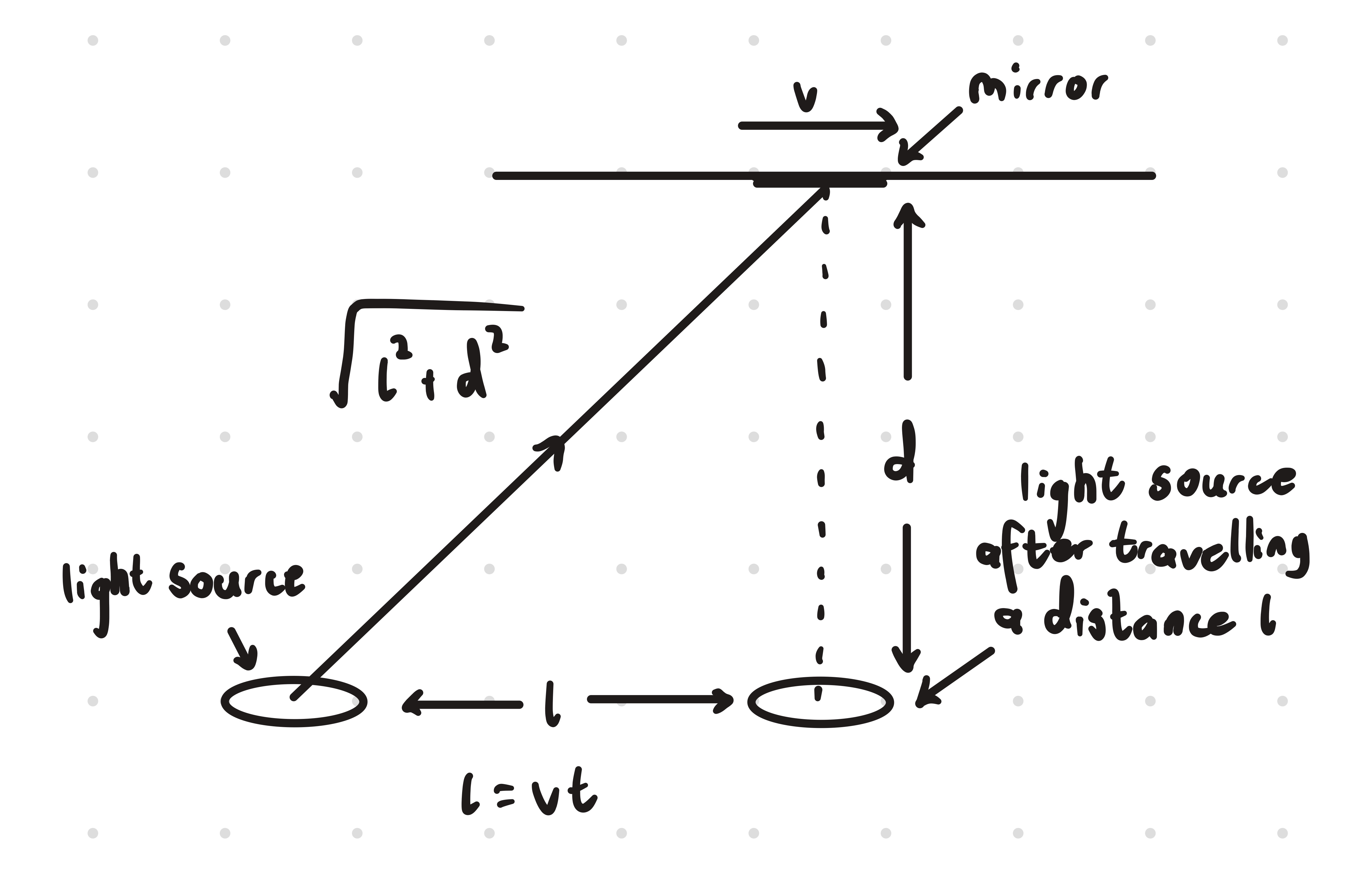
we can calculate

$$l = vt, \quad d=ct_0, \quad \sqrt{l^2 + d^2} = ct$$

subbing in $l$ and $d$

$$\sqrt{v^2t^2 + c^2t_0^2} = ct$$

solving for $t$ we get

$$t = \dfrac{t_0}{\sqrt{1 - \dfrac{v^2}{c^2}}}$$

or rewritten as

$$t = \gamma t_0$$

since

$$\gamma > 1$$

then

$$t > t_0$$

therefore more time has passed for the observer

 

Useful Equations

$$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}, \quad t = \gamma t_0$$

 

Example 1

A spacecraft travels at $0.6c$ relative to Earth. If $10$ seconds pass on a clock aboard the spacecraft, how much time passes on Earth?

Answer

calculate the Lorentz factor

$$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} = \frac{1}{\sqrt{1 - \frac{(0.6c)^2}{c^2}}} = \frac{1}{\sqrt{1 - 0.36}} = \frac{1}{\sqrt{0.64}} = \frac{1}{0.8} = 1.25$$

apply the time dilation formula

$$t = \gamma t_0 = 1.25 \times 10 = 12.5 \text{ s}$$

therefore $12.5$ seconds pass on Earth while $10$ seconds pass on the spacecraft

 

Example 2

A particle is accelerated to $0.95c$ in a laboratory. If the particle's internal clock measures $2.0 \times 10^{-6}$ s before it decays, how long does it appear to exist in the laboratory frame?

Answer

calculate the Lorentz factor

$$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} = \frac{1}{\sqrt{1 - \frac{(0.95c)^2}{c^2}}} = \frac{1}{\sqrt{1 - 0.9025}} = \frac{1}{\sqrt{0.0975}} \approx 3.20$$

apply the time dilation formula

$$t = \gamma t_0 = 3.20 \times 2.0 \times 10^{-6} = 6.4 \times 10^{-6} \text{ s}$$

the particle appears to exist for approximately $6.4 \times 10^{-6}$ s in the laboratory frame

 

Example 3

A GPS satellite orbits at a speed where $\gamma = 1.0000000001$. If $1$ day passes on the satellite, how much more time passes on Earth?

Answer

using $t = \gamma t_0$ with $t_0 = 1$ day

$$t = 1.0000000001 \times 1 = 1.0000000001 \text{ days}$$

the time difference is

$$\Delta t = t - t_0 = 1.0000000001 - 1 = 0.0000000001 \text{ days}$$

converting to microseconds ($1$ day $= 86400$ s)

$$\Delta t = 0.0000000001 \times 86400 \times 10^6 = 8.64 \text{ μs}$$

Earth clocks are ahead by approximately $8.64$ microseconds per day, which must be corrected for GPS accuracy